XGBoost是一个综合性的机器学习算法,可用于回归、分类和排序等各种问题,被广泛应用于机器学习竞赛和工业领域。成功案例包括:网页文本分类、客户行为预测、情感挖掘、广告点击率预测、恶意软件分类、项目分类、风险评估、大规模在线课程辍学率预测。XGBoost是初学者理解最深入的模型之一。连接了决策树、boosting、GBDT等知识点。强烈建议大家看看。在这篇文章中,我将从XGBoost的起源和优势、模型原理和优化推导、XGBoost模型参数分析、调参实例、XGBoost可视化等方面来介绍XGBoost。提醒一下,XGBoost是在GBDT基础上的改进。阅读本文需要对GBDT有一定的了解。不熟悉的同学可以看之前的文章:100天搞定机器学习|Day58机器学习入门:GBDTX优势硬核拆解在数据建模中,经常会用到Boosting的方法。该方法将数百个分类准确率低的树模型组合起来,成为准确率高的预测模型。这个模型会不断迭代,每次迭代都会生成一棵新树。但是,当数据集比较复杂时,可能需要进行数千次迭代操作,这会造成巨大的计算瓶颈。针对这一问题,华盛顿大学陈天奇博士开发的XGBoost(eXtremeGradientBoosting)基于C++通过多线程实现了回归树的并行构建,并对原有的GradientBoosting算法进行了改进,从而大大提高了模型训练速度和预测精度。XGBoost的主要优点如下:1.GBDT在优化时只使用一阶导数信息,XGBoost同时使用一阶和二阶导数信息,也支持自定义损失函数,前提是损失函数可以推导通过一阶和二阶导数;2、增加一个正则项,控制模型的复杂度,防止过拟合;3、借鉴随机森林的做法,支持列采样(随机选择特征),既可以减少过拟合,又可以减少计算量;4.在寻找最佳分割点时,实现了一种近似的方法,同时考虑了对稀疏数据集和缺失值的处理,大大提高了算法的效率;5.支持并行;6、近似直方图算法,高效生成候选分割点;7、在算法的实现上做了很多优化,大大提高了算法的效率。当内存空间不够时,采用阻塞、预取、压缩、多线程协同的思想。XGBoost模型原理和优化推导XGBoost其实是GBDT的一种,或者说是加法模型和前向优化算法。加性模型是指强分类器由一系列弱分类器线性相加而成。一般组合形式如下:$$F_M(x;P)=\sum_{m=1}^n\beta_mh(x;a_m)$$其中,$h(x;a_m)$为弱分类器一个接一个,$a_m$是弱分类器学习到的最优参数,$β_m$是弱学习在强分类器中的比例,P是所有$α_m$和$β_m$的组合。这些弱分类器线性相加形成强分类器。前向步进是指在训练过程中,在上一轮迭代的基础上训练下一轮迭代生成的分类器。即可以写成这样的形式:$$F_m(x)=F_{m-1}(x)+\beta_mh_m(x;a_m)$$XGBoost的模型是什么样的?$$\hat{y}_i=\sum_{k=1}^Kf_k(x_i),f_k\in\mathcal{F}$$其中K是树的数量。$f$是一棵回归树,$f(x)=w_{q(x)}$,满足$(q:R^m\rightarrowT,w\inR^T)$q表示每棵树的结构,它将一个训练样本实例映射到相应的叶子索引。T是树中叶子的数量。每一个都对应一个独立的树结构q和叶子权重w。$\mathcal{F}$是所有回归树的函数空间。与决策树不同,每个回归树在每个叶子上都包含一个连续的分数,我们用它来表示第i个叶子上的分数。对于给定的样本实例,我们将使用树上的决策规则(由q给出)将其分类到叶子上,并通过对相应叶子上的分数(由w给出)求和,计算出的最终预测值。XGBoost的学习为了在这个模型中学习这些函数集,我们将最小化以下正则化目标函数:$$\text{obj}(\theta)=\sum_i^nl(y_i,\hat{y}_i)+\sum_{k=1}^K\Omega(f_k)$$其中:$l$是损失函数,常见的有两种:平方损失函数:$l(yi,y^i)=(y_i?y^i)2$逻辑回归损失函数:$l(yi,y^i)=y_i\ln\left(1+e^{-\hat{y}_i}\right)+\left(1-y_i\right)\ln\left(1+e^{\hat{y}_i}\right)$$Ω(Θ)$:正则化项,用于惩罚复杂模型,避免模型对训练数据过拟合。常用的正则化有L1正则化和L2正则化:L1正则化(lasso):$Ω(w)=λ||w||_1$L2正则化:$Ω(w)=\lambda||w||^2$的第一步是学习目标函数,每次都保持原始模型不变,并向我们的模型添加一个新函数$f$。$$\begin{split}\hat{y}_i^{(0)}&=0\\hat{y}_i^{(1)}&=f_1(x_i)=\hat{y}_i^{(0)}+f_1(x_i)\\hat{y}_i^{(2)}&=f_1(x_i)+f_2(x_i)=\hat{y}_i^{(1)}+f_2(x_i)\&\点\\hat{y}_i^{(t)}&=\sum_{k=1}^tf_k(x_i)=\hat{y}_i^{(t-1)}+f_t(x_i)\end{split}$$其中,$\hat{y_i}^{(t)}$是第i个实例在第t次迭代时的预测,我们需要添加树$f_t$,然后最小化下面的目标函数:$$\begin{split}\text{obj}^{(t)}&=\sum_{i=1}^nl(y_i,\hat{y}_i^{(t)})+\sum_{i=1}^t\Omega(f_i)\\&=\sum_{i=1}^nl(y_i,\hat{y}_i^{(t-1)}+f_t(x_i))+\Omega(f_t)+\mathrm{constant}\end{split}$$假设损失函数使用平方损失$l(yi,y^i)=(y_i?y^i)2$,则上式进一步写为:$$\begin{split}\text{obj}^{(t)}&=\sum_{i=1}^n(y_i-(\hat{y}_i^{(t-1)}+f_t(x_i)))^2+\sum_{i=1}^t\Omega(f_i)\\&=\sum_{i=1}^n[2(\hat{y}_i^{(t-1)}-y_i)f_t(x_i)+f_t(x_i)^2]+\Omega(f_t)+\mathrm{常数}\end{split}$$现在,我们使用泰勒展开来定义一个近似的目标函数:$\text{obj}^{(t)}=\sum_{i=1}^n[l(y_i,\hat{y}_i^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+\Omega(f_t)+\mathrm{constant}$其中:$$\begin{split}g_i&=\partial_{\hat{y}_i^{(t-1)}}l(y_i,\hat{y}_i^{(t-1)})\h_i&=\partial_{\hat{y}_i^{(t-1)}}^2l(y_i,\hat{y}_i^{(t-1)})\end{split}$$$g_i,h_i$分别是损失函数上的一阶梯度和二阶梯度。忘本的同学复习泰勒公式会顺便提一下泰勒公式(Taylor'sFormula)是利用函数在某一点的信息来描述其附近值的公式。它的初衷是用多项式来逼近函数在某一点附近的情况。$x_0$处函数$f(x)$的基本形式如下$$\begin{align*}f(x)&=\sum_{n=0}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\&=f(x_0)+f^{1}(x_0)(x-x_0)+\frac{f^{2}(x_0)}{2}(x-x_0)^2+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\end{align*}$$还有一种常见的写法,$x^{t+1}=x^t+\Deltax$,泰勒在$x^t$展开$f(x^{t+1})$得到:$$\begin{align*}f(x^{t+1})&=f(x^t)+f^{1}(x^t)\Deltax+\frac{f^{2}(x^t)}{2}\Deltax^2+\cdots\end{align*}$$现在,让我们删除常量并重新访问我们的新目标函数:$$\sum_{i=1}^n[g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)]+\Omega(f_t)$$定义$I_j=\{i|q(x_i)=j\}$是叶A集合j的实例。$\Omega(f)=\gammaT+\frac{1}{2}\lambda\sum_{j=1}^Tw_j^2$引入正则项,展开目标函数:$$\begin{拆分}\text{obj}^{(t)}&\approx\sum_{i=1}^n[g_iw_{q(x_i)}+\frac{1}{2}h_iw_{q(x_i)}^2]+\gammaT+\frac{1}{2}\lambda\sum_{j=1}^Tw_j^2\\&=\sum^T_{j=1}[(\sum_{i\inI_j}g_i)w_j+\frac{1}{2}(\sum_{i\inI_j}h_i+\lambda)w_j^2]+\gammaT\end{split}$$看起来有点复杂,making:$G_j=\sum_{i\inI_j}g_i$,$H_j=\sum_{i\inI_j}h_i$,上式简化为:$$\text{obj}^{(t)}=\sum^T_{j=1}[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2]+\gammaT$$其中$w_j$相互独立,$G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2$是平方项。对于某个结构$q(x)$,我们可以计算出最优权重$w_j^{\ast}$:$$\begin{split}w_j^\ast&=-\frac{G_j}{H_j+\lambda}\\end{split}$$将$w_j^{\ast}$代入上式,计算出的loss最优解${obj}^*$:$$\begin{align*}Obj^{\(t)}&=\sum_{j=1}^T\left(G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2\right)+\gammaT\\&=\sum_{j=1}^T\left(-\frac{G_j^2}{H_j+\lambda}+\frac{1}{2}\frac{G_j^2}{H_j+\lambda}\right)+\gammaT\\&=-\frac{1}{2}\sum_{j=1}^T\left({\color{red}{\frac{G_j^2}{H_j+\lambda}}}}\right)+\gammaT\tag{2-8}\end{align*}$$${obj}^*$可以用作评分函数来衡量树结构$q(x)$的质量。我们有了衡量一棵树好坏的方法,现在我们来看XGBoost优化的第二个问题:如何选择分裂哪个特征和特征值,让我们最终的损失函数最小?XGBoost特征选择和分割点选择指标定义为:$$\begin{align*}gain=\underbrace{\frac{G_L^2}{H_L+\lambda}}_{leftnodescore}+\underbrace{\frac{G_R^2}{H_R+\lambda}}_{右节点得分}-\underbrace{\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}}_{分割前得分}-\gamma\end{align*}$$###如何精确拆分?**精确贪心算法**可用于枚举所有特征的所有可能分区。-尝试根据当前节点分裂决策树,默认score=0,G和H是当前需要分裂的节点的一阶导数和二阶导数之和。-Forfeaturenumberk=1,2...K:$G_L=0,H_L=0$-按照特征k从小到大排列样本,依次取第i个样本,计算当前样本依次放入左子树最后将左右子树的一阶导数和二阶导数求和:$G_L=G_L+g_{ti},G_R=G-G_L$$H_L=H_L+h_{ti},H_R=H-H_L$-尝试更新最大分数:$$score=max(score,\frac{1}{2}\frac{G_L^2}{H_L+\lambda}+\frac{1}{2}\frac{G_R^2}{H_R+\lambda}-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}-\gamma)$$-分割子树关于最大分值对应的划分特征和特征值。-如果最大分数为0,则建立当前决策树,计算所有叶子区域的$w_{tj}$,得到弱学习器$h_t(x)$,更新强学习器$f_t(x)$,并进入下一步一轮弱学习器迭代。如果最大分值不为0,继续尝试分裂决策树。###原理推导(精简版)下面是XGBoost原理推导的简化版,方便同学们复习和使用。$$\begin{align*}\begin{array}{l}\text{预测模型:}F(x)=\sum_{i=1}^Tw_if_i(x)\\text{目标函数:}obj^t=\sum_{i=1}^NL(y_i,F_i^t(x_i))+\Omega(f_t)\\因为obj^t=\sum_{i=1}^NL(y_i,F_i^t(x_i))+\Omega(f_t)\\\text{根据泰勒公式:}f(x+\Deltax)\thickapproxf(x)+\nablaf(x)\Deltax+\frac{1}{2}\nabla^2f(x)\Deltax^2\\因此obj^t\thickapprox\sum_{i=1}^N[L(y_i,F_i^{t-1}(x_i))+\nabla_{F_{t-1}}L(y_i,F_i^{t-1}(x_i))w_tf_t(x_i)\\text{使$g_i=\nabla_{F_{t-1}}L(y_i,F_i^{t-1}(x_i))$}\\\因为L(y_i,F_i^{t-1}(x_i))\text{是常数}\\\因此\text{目标函数:}\\\text{用叶子节点集和叶子节点分数表示,每个样本落在一个叶子节点上:}\f_t(x)=m_q(x),m\inR^T,q:R^d\rightarrow{1,2,3,...,T}\\Omega(f_t)=\gammaT+\frac{1}{2}\lambda\sum_{i=1}^Tm_j^2,\\text{$T$是$t$树的叶子节点总数}\\text{$m_j$是第j个叶子节点的权重}\\text{定义第$j$个叶子节点所在的样本为$I_j=\{i|j=q(x_i)\}$}\\text{新目标函数:}\obj^t=\sum_{i=1}^N[g_iw_tf_t(x_i)+\frac{1}{2}h_iw_t^2f_t^2(x_i)]+\Omega(f_t)\\text{顺序:$G_j=\sum_{i\inI_j}g_i$,$H_j=\sum_{i\inI_j}h_i$}\obj^t=\sum_{j=1}^吨[G_jw_tm_j+\frac{1}{2}(H_jw_t^2+\lambda)m_j^2]+\gammaT\\text{对于二次函数优化问题:}\m_j^*=-\frac{G_j^2w_t}{H_jw_t^2+\lambda}\obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2w_t^2}{H_jw_t^2+\lambda}+\伽玛T\\text{使$w_t=1$:}\m_j^*=-\frac{G_j}{H_j+\lambda}\obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda}+\gammaT\\text{所以当我们添加一个新的分割点时增益为:}\gain=\underbrace{\frac{G_L^2}{H_L+\lambda}}_{左节点得分}+\underbrace{\frac{G_R^2}{H_R+\lambda}}_{右节点得分}-\underbrace{\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}}_{scorebeforesegmentation}-\gamma\end{array}\end{align*}$$###Xgboost@sklearn模型参数分析有XGBoost原生版本和Scikit-learn版本,有两者在使用上有一些细微差别,这里是xgboost.sklearn参数解释XGBoost使用**key-value**字典来存储参数:```#Someimportantparametersparams={'booster':'gbtree','目标':'multi:softmax',#multi-categoryproblem'num_class':10,#类别数,与multisoftmax一起使用'gamma':0.1,#用于控制是否后剪枝的参数,值越大越保守,一般为0.1,0.2.'max_depth':12,#构造树的深度,越大越容易过拟合'lambda':2,#控制模型复杂度权重值的L2正则化项参数,参数越大,该模型不太可能过度拟合。'subsample':0.7,#随机采样训练样本'colsample_bytree':0.7,#生成树时列采样'min_child_weight':3,'silent':1,#设置为1,不输出运行信息,最好设置为0.'eta':0.007,#喜欢学习率'seed':1000,'nthread':4,#cpu线程数}```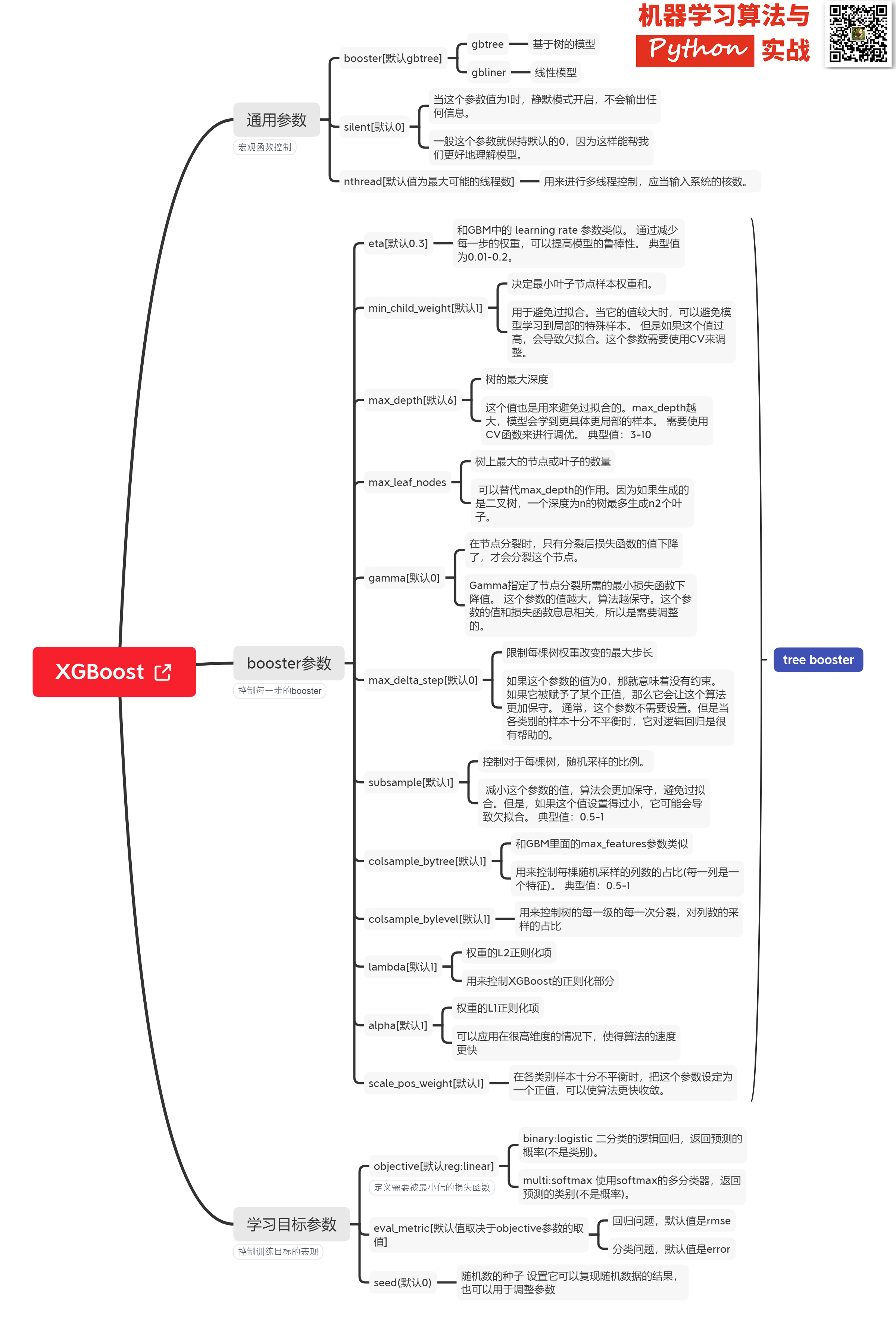限于篇幅,XGBoost参数调参和可视化的例子听下一章分解。如果有收获,欢迎给我一个**在看,收藏,转发**##参考https://www.cnblogs.com/pinard/p/10979808.htmlhttps://www.biaodianfu.com/xgboost.htmlhttps://www.zybuluo.com/vivounicorn/note/446479https://www.cnblogs.com/chenjieyouge/p/12026339.html
